
ABSTRACT
DISCIPLINA DELLE RESTITUZIONI CONTRATTUALI NEI FINANZIAMENTI RATEALI
Nel rinviare all’articolo INTERESSI LEGALI MAGGIORATI AI SENSI DELL’ART. 1284, COMMA 4, C.C. (C.D. INTERESSE COMMERCIALE EX D.LGS. 231/2002), all’articolo L’INDETERMINATEZZA CONTRATTUALE DEL SISTEMA “FRANCESE”, all’articolo È INEQUIVOCABILE CHE L’ART. 821 C.C. PRESCRIVE L’UTILIZZO DELLA FORMULA DEL PRINCIPIO DI EQUITÀ DEL REGIME SEMPLICE DELLA RATA COSTANTE POSTICIPATA e all’articolo IL SISTEMA FRANCESE DETERMINA IL REATO DI AUTORICICLAGGIO CON LA RESPONSABILITÀ PENALE DELL’INTERMEDIARIO EX D.LGS 231/2001, è indubitabile che i Bancari latu sensu quando concedono finanziamenti rateali sono in MALA FEDE perchè il loro dolo è provato “al di là di ogni ragionevole dubbio” ex art. 533, comma 1, c.p.p.: conseguentemente, gli interessi da pagare ai finanziati decorrono dal MOMENTO DEL PAGAMENTO e NON dal MOMENTO DELLA DOMANDA.
ALLE RESTITUZIONI CONTRATTUALI NEI FINANZIAMENTI RATEALI È APPLICABILE L’ART. 1284, COMMA 4, C.C.
Nel rinviare all’articolo CASSAZIONE CIVILE, ORDINANZA DEL 03-01-2023 N. 61, gli ermellini hanno affermato, in sintesi, che la mera azione di RIPETIZIONE DELL’INDEBITO esperita dal correntista, per ottenere la restituzione di importi illegittimamente trattenuti dalla propria banca sulla base di clausole contrattuali nulle, costituisce un’azione restitutoria che trova la sua base nel rapporto CONTRATTUALE tra istituto di credito e cliente. Infatti, si tratta di un’azione restitutoria relativa all’inadempimento di un accordo contrattuale e, di conseguenza, il relativo credito resta assoggettato alla disposizione di cui all’art. 1284, IV comma c.c..
COME SI DEVE APPLICARE IL COMBINATO DISPOSTO DEGLI ARTT. 1224 E 1284 CODICE CIVILE
Nel rinviare all’articolo CASSAZIONE CIVILE, ORDINANZA DEL 03-01-2023 N. 61, gli ermellini hanno affermato in questa ordinanza che “… (…) … si deve tenere conto del fatto che le previsioni di cui all’art. 1224 c.c. hanno ad oggetto il TASSO DI MORA nelle obbligazioni pecuniarie, cioè il tasso di interessi applicabile, in tale categoria di obbligazioni, dal giorno della mora (che può ovviamente essere anteriore a quello di inizio del processo), mentre l’art. 1284 c.c., comma 4, riguarda invece solo il TASSO DEGLI INTERESSI DI MORA per il periodo successivo all’inizio del processo: le due disposizioni hanno, quindi, un campo di applicazione differente, il che esclude che possano essere una la duplicazione dell’altra.
SI DETERMINA L’APPLICAZIONE DELL’ART. 1284, COMMA 4, C.C. NEL PROCESSO DI COGNIZIONE E NON NEL PROCEDIMENTO ESECUTIVO
Nel rinviare all’articolo INTERESSI LEGALI MAGGIORATI AI SENSI DELL’ART. 1284, COMMA 4, C.C. (C.D. INTERESSE COMMERCIALE EX D.LGS. 231/2002), sia con la sentenza della Cassazione Civile Sez. Unite del 07/05/2024 n. 12449 sia con la sentenza di Cassazione del 23/04/2020, n. 8128 sia con la sentenza di Cassazione del 04/08/2023, n. 23846, i giudici di legittimità hanno affermato che, in tema di ESECUZIONE FORZATA fondata su titolo esecutivo giudiziale, il giudice dell’esecuzione non ha poteri di cognizione e di accertamento dei fatti, ma deve limitarsi ad attuare il comando contenuto nel titolo esecutivo.
ARTICOLO
Preliminarmente, nel rinviare all’articolo CASSAZIONE CIVILE SEZIONI UNITE, SENTENZA DEL 07-05-2024 N. 12449, si evidenzia che gli Ermellini hanno stabilito che con l’espressione “interessi legali”, in assenza di specificazione, deve intendersi la misura degli interessi prevista dal primo comma dell’art. 1284 c.c. e NON quella da utilizzarsi nelle transazioni commerciali di cui al quarto comma dell’art. 1284 c.c.. Ne deriva che, se il titolo esecutivo è silente, il creditore non può conseguire in sede esecutiva il pagamento di “interessi legali maggiorati”, quali quelli previsti dal quarto comma dell’art. 1284 c.c. (stante l’impossibilità del giudice dell’ESECUZIONE di integrare il titolo), ma deve ricorrere al rimedio dell’impugnazione.
Nel rinviare all’articolo CASSAZIONE CIVILE, ORDINANZA DEL 08-09-2021 N. 24181, all’articolo CASSAZIONE CIVILE, ORDINANZA DEL 03-01-2023 N. 61 e all’articolo INTERESSI LEGALI MAGGIORATI AI SENSI DELL’ART. 1284, COMMA 4, C.C. (C.D. INTERESSE COMMERCIALE EX D.LGS. 231/2002), l’art. 1224 c.c. rubricato “Danni nelle obbligazioni pecuniarie” stabilisce che “Nelle obbligazioni che hanno per oggetto una somma di danaro, sono dovuti dal giorno della mora gli interessi legali, anche se non erano dovuti precedentemente e anche se il creditore non prova di aver sofferto alcun danno. Se prima della mora erano dovuti interessi in misura superiore a quella legale, gli interessi moratori sono dovuti nella stessa misura. Al creditore che dimostra di aver subito un danno maggiore spetta l’ulteriore risarcimento. Questo non è dovuto se è stata convenuta la misura degli interessi moratori”. La norma, com’è evidente, presuppone che la produzione di INTERESSI MORATORI sia subordinata alla costituzione in mora del debitore. L’art. 1219, comma 2, numero 3, c.c. stabilisce che “Non è necessaria la costituzione in mora: 1) … (…) …; 2) … (…) …; 3) quando è scaduto il termine, se la prestazione deve essere eseguita al domicilio del creditore”: pertanto, la costituzione in mora è automatica per i DEBITI PORTABILI, tra i quali rientrano quelli aventi ad oggetto una somma di denaro. Quanto ai CONTRATTI DI FINANZIAMENTO CON PIANO DI RIMBORSO RATEALE, il termine, cioè “il tempo in cui la prestazione deve essere eseguita” ex art. 1183 c.c., si compie il giorno di scadenza di ciascuna rata per i contratti in essere.
Strettamente correlata alla produzione di INTERESSI MORATORI ex art. 1224 c.c. è la disciplina dell’ANATOCISMO di tipo “SCADUTO” dell’art. 1283 c.c. e della Delibera CICR del 09/02/2000 n. 224000 “Modalità e criteri per la produzione di interessi sugli interessi scaduti” in vigore dal 22/04/2000 al 30/09/2015 che ha consentito ulteriori deroghe oltre ai casi specificati ex art. 1283 c.c..
Nel sottolineare che nell’ambito di applicazione dell’art. 1283 c.c. vi è pure l’ANATOCISMO degli INTERESSI DI MORA sugli INTERESSI MORATORI anche quando quest’ultimi sono formalmente qualificati dalle parti come CLAUSOLA PENALE (Cassazione Civile, Sez. Lavoro del 24/05/1986 n. 3500; Cassazione Civile del 13/12/2002 n. 17813) [1], in merito all’ANATOCISMO degli INTERESSI DI MORA sulle QUOTE INTERESSE CORRISPETTIVO “NON PAGATE” si evidenzia che solo nel caso in cui i finanziati non paghino regolarmente il prestito rateale, la singola QUOTA INTERESSE della rata non pagata scade matematicamente e, su questa singola QUOTA INTERESSE CORRISPETTIVO scaduta, si possono calcolare gli INTERESSI DI MORA se la normativa vigente lo consente.
In particolare, si evidenzia nel Paragrafo 9 del Volume II che il BANCARIO latu sensu è inequivocabilmente a conoscenza che la giurisprudenza di legittimità è ferma nel ritenere che sono senz’altro applicabili le limitazioni previste dall’art. 1283 c.c. sia ai contratti di MUTUO ORDINARIO sia a quelli di MUTUO FONDIARIO, non rilevando, in senso opposto, l’esistenza di un uso bancario contrario a quanto disposto da tale norma. Conseguentemente, i dirigenti e i dipendenti degli intermediari hanno la consapevolezza che:
1) nel periodo antecedente lo 01/01/1994 devono applicare ai contratti di MUTUO ORDINARIO le regole stabilite dall’art. 1283 c.c. mentre alle convenzioni di MUTUO FONDIARO si devono impiegare le disposizioni della LEGISLAZIONE SPECIALE[2];
2) Nel periodo fra lo 01/01/1994 e il 21/04/2000 si devono applicare sia ai contratti di MUTUO ORDINARIO sia a quelli di MUTUO FONDIARO le regole stabilite dall’art. 1283 c.c.;
3) Nel periodo fra il 22/04/2000 e il 31/12/2013 si devono adoperare sia per i contratti di MUTUO ORDINARIO sia per quelli di MUTUO FONDIARO le disposizioni della Delibera del CICR del 09/02/2000 n. 224000 in vigore dal 22/04/2000 al 30/09/2015 previste espressamente per QUALSIASI TIPO DI FINANZIAMENTO RATEALE[3];
4) Nel periodo fra lo 01/01/2014 e il 30/09/2015 si devono applicare sia ai contratti di MUTUO ORDINARIO sia a quelli di MUTUO FONDIARO le regole dell’art. 1283 c.c. perché le disposizioni della Delibera del CICR del 09/02/2000 n. 224000 in vigore dal 22/04/2000 al 30/09/2015 sono di fatto inefficaci dal 01/01/2014 poiché, dopo l’intervento sull’art. 120 del TUB da parte della Legge 27/12/2013, n. 147, la giurisprudenza maggioritaria ha affermato che tale norma esclude “inequivocabilmente la possibilità di praticare ulteriormente l’anatocismo bancario” in quanto la stessa è “immediatamente precettiva (o, secondo l’anglismo utilizzato dalla resistente, self executing), ancorché il CICR (che ne è stato incaricato) non abbia ancora provveduto a precisare modalità di contabilità bancaria destinati a dare attuazione al principio imperativamente espresso. Proprio la non essenzialità di ulteriore specificazione del chiaro principio di cui sopra (divieto di anatocismo bancario) impone di ritenere la norma de qua in vigore dall’1.1.2014”;
5) Nel periodo fra lo 01/10/2015 e il 14/04/2016 si devono adoperare sia per i contratti di MUTUO ORDINARIO sia per quelli di MUTUO FONDIARO le regole dell’art. 1283 c.c. poiché il Provvedimento della Banca d’Italia del 15/07/2015 n. 87795 (in GU del 29/07/15 n. 174) in vigore dal 01/10/2015 al 31/10/2016 in tema di “Trasparenza delle operazioni e dei servizi bancari e finanziari – correttezza delle relazioni tra intermediari e clienti”, ha eliminato con decorrenza dallo 01/10/2015 il riferimento tra le “fonti normative” della Delibera del CICR del 09/02/2000 n. 224000 in vigore dal 22/04/2000 al 30/09/2015 indipendentemente dall’emanazione di una delibera sostitutiva ex art. 120, comma 2, del TUB in vigore dallo 01/01/2014 al 14/04/2016;
6) Nel periodo fra il 15/04/2016 e il 30/09/2016 si devono applicare sia ai contratti di MUTUO ORDINARIO sia a quelli di MUTUO FONDIARO le regole dell’art. 1283 c.c. perché nell’art. 120 del TUB in vigore dal 15/04/2016 nulla si dice espressamente sulla disciplina applicabile per il conteggio degli INTERESSI DI MORA sia sulla QUOTA INTERESSE CORRISPETTIVO “NON PAGATA” della rata non effettivamente rimborsata di QUALSIASI TIPO DI FINANZIAMENTO RATEALE sia in merito all’ANATOCISMO degli INTERESSI DI MORA sugli INTERESSI MORATORI;
7) Nel periodo dallo 01/10/2016 ad oggi si devono adoperare sia per i contratti di MUTUO ORDINARIO sia per quelli di MUTUO FONDIARO le regole dell’art. 1283 c.c. perché la Delibera del CICR del 03/08/2016 n. 103824 (in G.U. del 10/09/16 n. 212) in vigore dal 01/10/2016 stabilisce espressamente all’art. 3, comma 2, che “agli INTERESSI MORATORI si applicano le disposizioni del codice civile” per QUALSIASI TIPO DI FINANZIAMENTO RATEALE.
Pertanto, quando ai contratti di FINANZIAMENTO CON PIANO DI RIMBORSO RATEALE si deve applicare temporalmente la disciplina codicistica dell’ANATOCISMO di tipo “SCADUTO” ex art. 1283 c.c., valgono i principi di diritto sanciti dalla sentenza della Cassazione Civile del 20/02/2003 n. 2593[4], della Cassazione Civile, Sez. Lavoro del 24/05/1986 n. 3500 e della Cassazione Civile del 13/12/2002 n. 17813 [1] che possono essere così sintetizzati:
a) È nulla per violazione dell’art. 1283 c.c. la clausola inserita nella convenzione al momento della conclusione del contratto che stabilisce espressamente il calcolo dell’INTERESSE MORATORIO sull’importo complessivo della RATA “NON PAGATA”, cioè il conteggio della MORA sia sul valore della sua specifica QUOTA CAPITALE ridistribuita nel PDA dall’imposizione del vincolo matematico del DEBITO RESIDUO equo sia sul valore della sua corrispondente QUOTA INTERESSE individuata per differenza con la rata costante posticipata attraverso l’equazione RATA meno QUOTA CAPITALE, in quanto questa postilla pattizia è in contrasto con la disposizione del codice civile che non ammette patti anteriori alla scadenza giuridica degli INTERESSI CORRISPETTIVI;
b) È valida ex art. 1283 c.c. la clausola inserita nella convenzione al momento della conclusione del contratto che stabilisce espressamente il calcolo dell’INTERESSE MORATORIO sul solo importo della specifica QUOTA CAPITALE della RATA “NON PAGATA”. Ovviamente, tale QUOTA CAPITALE deve essere, ex art. 821, comma 3, c.c., quella del PDA LINEARE “ANNO CIVILE CORRETTO” conseguenziale all’applicazione della formula del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE con la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO”;
c) è consentito l’ANATOCISMO degli INTERESSI DI MORA sugli INTERESSI MORATORI anche quando quest’ultimi sono formalmente qualificati dalle parti come CLAUSOLA PENALE.
In caso di RISOLUZIONE del contratto di finanziamento rateale, nella vigenza della LEGISLAZIONE SPECIALE ex art. 15 del D.P.R. del 21/01/1976 n. 7 la sentenza della Cassazione Civile Sez. Un. del 19/05/2008 n. 12639 ha stabilito per un contratto di MUTUO FONDIARIO stipulato nel vigore dello stesso decreto che il cliente deve provvedere “all’immediata restituzione della quota di capitale ancora dovuta, ma non al pagamento degli interessi conglobati nella semestralità a scadere, dovendosi invece calcolare, sul credito così determinato, gli INTERESSI DI MORA a un tasso corrispondente a quello contrattualmente pattuito, se superiore al tasso legale, secondo quanto previsto dall’art. 1224, 1° comma, c.c..”. Ciò significa che gli INTERESSI DI MORA debbono essere calcolati oltre che sulla complessiva COMPONENTE CAPITALE non rimborsata anche sulle QUOTE INTERESSE CORRISPETTIVO “NON PAGATE” delle sole rate effettivamente non restituite prima della risoluzione.
La Delibera CICR del 09/02/2000 n. 224000 “Modalità e criteri per la produzione di interessi sugli interessi scaduti” in vigore dal 22/04/2000 al 30/09/2015 (di fatto inefficace dal 01/01/2014) ha mantenuto la legittimità codicistica ex art. 1224 c.c. del conteggio degli INTERESSI DI MORA sulla COMPONENTE CAPITALE complessivamente dovuta “a decorrere dalla data di risoluzione”, ma ha stabilito che sull’importo di questa MORA non è consentita “la capitalizzazione periodica”. In altre parole, è possibile, ad esempio, il conteggio degli INTERESSI DI MORA oltre che sulle QUOTE CAPITALE delle sette rate consecutive impagate ex art. 40, comma 2, del TUB [5] anche sul DEBITO RESIDUO precedente la prima rata impagata delle sette NON consecutive: naturalmente, sia le QUOTE CAPITALE che il DEBITO RESIDUO equo devono essere quelli del PDA LINEARE “ANNO CIVILE CORRETTO” ex art. 1374 c.c.. Quanto agli INTERESSI DI MORA da calcolare nei FINANZIAMENTI RATEALI e nei CONTI CORRENTI, con il combinato disposto dell’art. 5 rubricato “Domanda giudiziale e convenzioni posteriori alla scadenza” che prevede che “1. Gli interessi scaduti possono produrre interessi, oltre che nelle ipotesi e secondo le modalità di cui ai precedenti articoli, dal giorno della domanda giudiziale o per effetto di convenzione posteriore alla scadenza e sempre che si tratti di interessi dovuti per almeno sei mesi” e degli artt. 2 e 3 che prevedono che sull’importo della MORA “non è consentita la capitalizzazione periodica”, la Delibera del 2000 stabilisce un generale divieto di ANATOCISMO di tipo “SCADUTO” sull’importo degli INTERESSI MORATORI conteggiati. Conseguentemente, a far data dal 22/04/2000, l’ANATOCISMO di tipo “SCADUTO” nei casi previsti dall’art. 5 è applicabile solo agli INTERESSI CORRISPETTIVI matematicamente scaduti e, quindi, all’art. 5 non è riferibile la giurisprudenza consolidata dell’art. 1283 c.c. che prevede che l’ambito di applicazione della norma codicistica comprende l’ANATOCISMO degli INTERESSI DI MORA sugli INTERESSI MORATORI.
Nel ricordare che nella vigenza dell’art. 1283 c.c. è consentito l’ANATOCISMO degli INTERESSI DI MORA sugli INTERESSI MORATORI anche quando quest’ultimi sono formalmente qualificati dalle parti come CLAUSOLA PENALE, alla luce della normativa appena descritta devono essere valutati i principi di diritto enunciati dalla sentenza della Cassazione Civile, Sezioni Unite, del 18/09/2020 n. 19597 che nella fattispecie concreta aveva per oggetto “un finanziamento concesso con un contratto di credito al consumo stipulato il 23 aprile 2002”.
In altre parole, i principi di diritto delle Sezioni Unite del 2020 non possono valere indistintamente in OGNI TEMPO ed in OGNI CASO perché vige nel nostro ordinamento civile il brocardo tempus regit actum che sintetizza i principi di irretroattività (la norma giuridica civile non si applica a fatti o rapporti sorti prima della sua entrata in vigore) e di non ultrattività della legge (la norma giuridica non si applica ai fatti verificatisi dopo la sua estinzione). In particolare ci si riferisce ai seguenti principi di diritto:
- Nel punto v), le Sezioni Unite del 2020 hanno stabilito per i finanziamenti rateali che in caso di USURARIETÀ dei soli INTERESSI MORATORI, “le rate SCADUTE al momento della caducazione del prestito restano dovute nella loro integralità, comprensive degli INTERESSI CORRISPETTIVI in esse conglobati, oltre agli INTERESSI MORATORI sull’intero nella misura dei CORRISPETTIVI pattuiti; tale effetto, peraltro, richiede che in sé il TASSO degli INTERESSI CORRISPETTIVI sia lecito. Per quanto attiene le rate A SCADERE, sorge l’obbligo d’immediata restituzione dell’intero capitale ricevuto, sul quale saranno dovuti gli INTERESSI CORRISPETTIVI, ma attualizzati al momento della risoluzione: infatti, fino al momento in cui il contratto ha avuto effetto, il debitore ha beneficiato della rateizzazione, della quale deve sostenere il costo, pur ricalcolato attualizzandolo, rispetto all’originario piano di ammortamento non più eseguito; da tale momento e sino al pagamento, vale l’art. 1224, comma 1, c.c.“. In altre parole, in caso di USURARIETÀ dei soli INTERESSI MORATORI, per le Sezioni Unite del 2020, al momento della risoluzione, l’importo complessivo da restituire è dato dalla somma dei seguenti addendi: 1) rate SCADUTE NON PAGATE; 2) rate A SCADERE ATTUALIZZATE al TASSO CONTRATTUALE degli INTERESSI CORRISPETTIVI lecito; 3) INTERESSI MORATORI calcolati sulle rate SCADUTE NON PAGATE al TASSO CONTRATTUALE degli INTERESSI CORRISPETTIVI lecito: ovviamente, “da tale momento e sino al pagamento, vale l’art. 1224, comma 1, c.c.“ e, cioè, sull’importo complessivo così calcolato al momento della risoluzione, devono essere conteggiati ULTERIORI INTERESSI al TASSO LEGALE o al TASSO CONTRATTUALE degli INTERESSI CORRISPETTIVI lecito se più alto. Conseguentemente, se il TASSO CONTRATTUALE degli INTERESSI CORRISPETTIVI è illecito per la commissione del reato-mezzo di TRUFFA CONTRATTUALE e del reato-fine di USURA DEGLI INTERESSI CORRISPETTIVI IN SEDE CONTRATTUALE, in caso di USURARIETÀ anche degli INTERESSI MORATORI, l’importo complessivo da restituire è dato dalla somma dei seguenti addendi: 1) QUOTA CAPITALE delle rate SCADUTE NON PAGATE; 2) QUOTA CAPITALE delle rate A SCADERE; 3) INTERESSI MORATORI calcolati sulla QUOTA CAPITALE delle rate SCADUTE NON PAGATE al TASSO degli INTERESSI CORRISPETTIVI illecito, e cioè al TASSO dello ZERO%: ovviamente, “da tale momento e sino al pagamento, vale l’art. 1224, comma 1, c.c.“ e, cioè, sull’importo complessivo così calcolato al momento della risoluzione, devono essere conteggiati ULTERIORI INTERESSI al TASSO LEGALE perché il TASSO degli INTERESSI CORRISPETTIVI è illecito e, quindi, è un TASSO pari allo ZERO%;
- Nel punto vi), le Sezioni Unite del 2020 distinguono fra TASSO DI MORA ASTRATTO, cioè quello previsto in contratto, e TASSO DI MORA IN CONCRETO APPLICATO dando rilevanza sia al rapporto con pagamenti regolari sia al rapporto con inadempimenti di pagamento. Si legge nelle motivazioni che “se il finanziato agisce in accertamento in corso di REGOLARE RAPPORTO ed ottenga sentenza di nullità della clausola (degli INTERESSI MORATORI), ciò non vuol dire che, da quel momento in poi, egli potrà non adempiere e pretendere che nessun interesse gli sia applicato, oltre all’INTERESSE CORRISPETTIVO (lecito), incluso nelle rate già dovute”. In altre parole, per le Sezioni Unite del 2020 “ciò che rileva in concreto in ipotesi di INADEMPIMENTO è il TASSO MORATORIO APPLICATO” anche nel caso di sussistenza di una sentenza precedente che abbia dichiarato l’USURARIETÀ del TASSO DI MORA ASTRATTO, cioè quello previsto in contratto. Infatti, “tale sentenza non avrà ancora l’effetto concreto di rendere dovuto solo un INTERESSE MORATORIO pari al TASSO degli INTERESSI CORRISPETTIVI lecitamente pattuiti (ex art. 1224 cod-civ.): effetto che, invece, si potrà verificare solo alla condizione” che il TASSO DI MORA ASTRATTO riconosciuto giudizialmente USURARIO “sia stato, in seguito, il TASSO (MORATORIO) EFFETTIVAMENTE APPLICATO, o comunque che, al momento della MORA EFFETTIVA, il TASSO (MORATORIO) APPLICATO sulla base della clausola degli INTERESSI MORATORI sia sopra soglia. Ove il TASSO (MORATORIO) IN CONCRETO sia invece sotto soglia, esso sarà dovuto senza che possa farsi valere la sentenza di mero accertamento, che non quello ha considerato.” Conseguentemente, se il TASSO CONTRATTUALE degli INTERESSI CORRISPETTIVI è illecito per la commissione del reato-mezzo di TRUFFA CONTRATTUALE e del reato-fine di USURA DEGLI INTERESSI CORRISPETTIVI IN SEDE CONTRATTUALE, in caso di USURARIETÀ riconosciuta giudizialmente anche del TASSO DI MORA ASTRATTO CONTRATTUALE, gli INTERESSI MORATORI devono essere calcolati al TASSO degli INTERESSI CORRISPETTIVI illecito, e cioè al TASSO dello ZERO%. Nulla dicono espressamente le Sezioni Unite del 2020 sugli effetti sul TASSO DI MORA IN CONCRETO se il TASSO CONTRATTUALE degli INTERESSI CORRISPETTIVI è illecito di fatto o per sentenza precedente per la commissione del reato-mezzo di TRUFFA CONTRATTUALE e del reato-fine di USURA DEGLI INTERESSI CORRISPETTIVI IN SEDE CONTRATTUALE: 1) dall’interpretazione letterale delle motivazioni, è inevitabile che l’usurarietà degli INTERESSI MORATORI EFFETTIVI, sia nel caso in cui il loro TASSO sia identico al TASSO DI MORA ASTRATTO riconosciuto da una sentenza precedente illecito sia nel caso in cui il loro TASSO sia sopra soglia al momento del pagamento effettivo inadempiuto, devono essere calcolati al TASSO degli INTERESSI CORRISPETTIVI illecito, e cioè al TASSO dello ZERO%; 2) dall’interpretazione logica delle motivazioni, è plausibile che la NON USURARIETÀ degli INTERESSI MORATORI EFFETTIVI perchè conteggiati dall’intermediario con un TASSO sotto soglia al momento del pagamento effettivo inadempiuto, devono essere calcolati al TASSO degli INTERESSI CORRISPETTIVI illecito, e cioè al TASSO dello ZERO%, anche perchè, altrimenti, i Bancari latu sensu incasserebbero ulteriori INTERESSI CORRISPETTIVI truffaldini “mascherati” fittiziamente e artatamente come INTERESSI MORATORI in quanto conteggiati sulla rata costante posticipata dell’AMMORTAMENTO “FRANCESE” o sulla rata variabile posticipata dell’AMMORTAMENTO “ITALIANO” calcolate nell’illecito REGIME COMPOSTO.
In considerazione che il TASSO ANNUO dell’interesse MORATORIO deve essere rimborsato in un’unica soluzione sull’intero importo dovuto, il calcolo dell’importo della MORA deve essere fatto con la formula del MONTANTE.
Se NON si riconosce la violazione dell’art. 821, comma 3, c.c. che impone anche il REGIME SEMPLICE, quandola normativa dell’art. 1283 c.c. è vigente e, quindi, la stessa consente l’ANATOCISMO degli INTERESSI DI MORA sugli INTERESSI MORATORI, può essere utilizzata anche la formula del MONTANTE del REGIME COMPOSTO che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO”
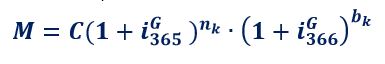
con i tassi giornalieri equivalenti dell’anno normale di 365 giorni e dell’anno bisestile di 366 giorni calcolati con la formula del principio di equivalenza
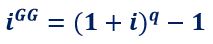
in conformità con la Normativa di Trasparenza Banca d’Italia vigente che prevede sia il metodo di conteggio dell’ANNO CIVILE “CORRETTO” sia i tassi giornalieri equivalenti.
Se si riconosce la violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, si deve impiegare la formula del MONTANTE del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO”
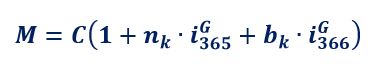
con i tassi giornalieri equivalenti dell’anno normale di 365 giorni e dell’anno bisestile di 366 giorni calcolati con la formula del principio di equivalenza
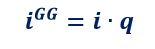
Le formule del MONTANTE sono illustrate nel Paragrafo 2 del Volume I.
In merito alla quantificazione degli INTERESSI MORATORI in caso di RISOLUZIONE del contratto di finanziamento rateale occorre mostrare che sussistono diverse MODALITÀ DI CONTEGGIO dell’importo della MORA dovuta:
- Nella eventualità che NON sia riconosciuta giudizialmente né l’INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO, né la violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, né l’INDETERMINATEZZA CONTRATTUALE in GENERALE, nel REGIME COMPOSTO e nel REGIME SEMPLICE della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO, né l’USURARIETÀ strettamente connessa al TASSO MORATORIO che non tiene conto dei costi inerenti alla fase fisiologica, né l’USURARIETÀ strettamente connessa al TASSO CORRISPETTIVO che non tiene conto dei costi inerenti alla fase patologica, né l’ERRONEITÀ della percentuale del TAEG contrattuale, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva determinata dal BANCARIO latu sensu nel REGIME COMPOSTO. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando il TASSO ANNUO MORATORIO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente la sola violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando il TASSO ANNUO MORATORIO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente la sola INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva determinata dal BANCARIO latu sensu nel REGIME COMPOSTO. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando il TASSO ANNUO CORRISPETTIVO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO insieme alla violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando il TASSO ANNUO CORRISPETTIVO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente la sola USURARIETÀ strettamente connessa al TASSO MORATORIO che non tiene conto dei costi inerenti alla fase fisiologica, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva determinata dal BANCARIO latu sensu nel REGIME COMPOSTO. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando il TASSO ANNUO CORRISPETTIVO contrattuale EFFETTIVO come indicato nella sentenza della Cassazione Civile, Sezioni Unite, del 18/09/2020 n. 19597.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’USURARIETÀ strettamente connessa al TASSO MORATORIO che non tiene conto dei costi inerenti alla fase fisiologica insieme alla violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando il TASSO ANNUO CORRISPETTIVO contrattuale EFFETTIVO come indicato nella sentenza della Cassazione Civile, Sezioni Unite, del 18/09/2020 n. 19597.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente la sola ERRONEITÀ della percentuale del TAEG contrattuale, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva derivante dall’applicazione con l’equazione del PRINCIPIO DI EQUITÀ del REGIME COMPOSTO della SANZIONE CIVILE del TASSO BOT MINIMO dell’art. 124 o dell’art. 125-bis del TUB. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando il TASSO ANNUO MORATORIO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’ERRONEITÀ della percentuale del TAEG contrattuale insieme all’INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva derivante dall’applicazione con l’equazione del PRINCIPIO DI EQUITÀ del REGIME COMPOSTO della SANZIONE CIVILE del TASSO BOT MINIMO dell’art. 124 o dell’art. 125-bis del TUB. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando il TASSO ANNUO CORRISPETTIVO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’ERRONEITÀ della percentuale del TAEG contrattuale insieme alla violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata della SANZIONE CIVILE del TASSO BOT MINIMO dell’art. 124 o dell’art. 125-bis del TUB con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando il TASSO ANNUO MORATORIO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’ERRONEITÀ della percentuale del TAEG contrattuale insieme all’INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO e alla violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata della SANZIONE CIVILE del TASSO BOT MINIMO dell’art. 124 o dell’art. 125-bis del TUB con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando il TASSO ANNUO CORRISPETTIVO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente la sola INDETERMINATEZZA CONTRATTUALE in GENERALE o nel REGIME COMPOSTO della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva derivante dall’applicazione con l’equazione del PRINCIPIO DI EQUITÀ del REGIME COMPOSTO della SANZIONE CIVILE del TASSO LEGALE VIGENTE dell’art. 1284 c.c.. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando il TASSO ANNUO MORATORIO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’INDETERMINATEZZA CONTRATTUALE in GENERALE o nel REGIME COMPOSTO della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO insieme all’INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO, si deve usare la somma complessiva derivante dall’applicazione con l’equazione del PRINCIPIO DI EQUITÀ del REGIME COMPOSTO della SANZIONE CIVILE del TASSO LEGALE VIGENTE dell’art. 1284 c.c.. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando l’aliquota media del TASSO LEGALE VIGENTE.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’INDETERMINATEZZA CONTRATTUALE in GENERALE, nel REGIME COMPOSTO e nel REGIME SEMPLICE della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO insieme alla violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata della SANZIONE CIVILE del TASSO LEGALE VIGENTE dell’art. 1284 c.c. con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando il TASSO ANNUO MORATORIO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’INDETERMINATEZZA CONTRATTUALE in GENERALE, nel REGIME COMPOSTO e nel REGIME SEMPLICE della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO insieme alla violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO” e all’INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata della SANZIONE CIVILE del TASSO LEGALE VIGENTE dell’art. 1284 c.c. con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando l’aliquota media del TASSO LEGALE VIGENTE.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente la sola INDETERMINATEZZA CONTRATTUALE in GENERALE o nel REGIME COMPOSTO della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva derivante dall’applicazione con l’equazione del PRINCIPIO DI EQUITÀ del REGIME COMPOSTO della SANZIONE CIVILE del TASSO BOT MINIMO dell’art. 117, comma 7 del TUB. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando il TASSO ANNUO MORATORIO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’INDETERMINATEZZA CONTRATTUALE in GENERALE o nel REGIME COMPOSTO della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO insieme all’INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO, si deve usare la somma complessiva derivante dall’applicazione con l’equazione del PRINCIPIO DI EQUITÀ del REGIME COMPOSTO della SANZIONE CIVILE del TASSO BOT MINIMO dell’art. 117, comma 7 del TUB. In questo caso, per determinare l’importo della MORA si deve/può utilizzare, in analogia matematica, la formula del MONTANTE del REGIME COMPOSTO impiegando l’aliquota media del TASSO LEGALE VIGENTE.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’INDETERMINATEZZA CONTRATTUALE in GENERALE, nel REGIME COMPOSTO e nel REGIME SEMPLICE della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO insieme alla violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO”, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata della SANZIONE CIVILE del TASSO BOT MINIMO dell’art. 117, comma 7 del TUB con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando il TASSO ANNUO MORATORIO contrattuale.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente l’INDETERMINATEZZA CONTRATTUALE in GENERALE, nel REGIME COMPOSTO e nel REGIME SEMPLICE della clausola pattizia relativa al TASSO ANNUO dell’interesse CORRISPETTIVO insieme alla violazione dell’art. 821, comma 3, c.c. che impone il REGIME SEMPLICE e il metodo di conteggio dell’ANNO CIVILE “CORRETTO” e all’INDETERMINATEZZA CONTRATTUALE in GENERALE della clausola pattizia relativa al TASSO ANNUO dell’interesse MORATORIO, quanto all’individuazione dell’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” si deve usare la somma complessiva che si determina decretando ai sensi del combinato disposto degli artt. 1374 e 1419, comma 2, c.c. il ricalcolo della rata costante posticipata della SANZIONE CIVILE del TASSO BOT MINIMO dell’art. 117, comma 7 del TUB con l’equazione del PRINCIPIO DI EQUITÀ con impostazione iniziale in t_0 del REGIME SEMPLICE che usa la ponderazione dei periodi rateali dell’ANNO CIVILE “CORRETTO” e i tassi giornalieri equivalenti. In questo caso, per determinare l’importo della MORA si deve utilizzare la formula del MONTANTE del REGIME SEMPLICE impiegando l’aliquota media del TASSO LEGALE VIGENTE.
- Se nella combinazione descritta nel punto a) è riconosciuta giudizialmente la sola USURARIETÀ strettamente connessa al TASSO CORRISPETTIVO che non tiene conto dei costi inerenti alla fase patologica, NON è necessario individuare l’importo del “capitale scaduto e residuo a scadere e gli interessi maturati” perché NON sussiste la necessità normativa di determinazione dell’importo della MORA. Infatti, alla luce del principio di unitarietà e di non contraddizione dell’ordinamento giuridico, l’interpretazione sistematica che rispetta le finalità perseguite dalla norma penale e coglie le connessioni concettuali esistenti fra la norma penalistica dell’art. 644, comma 4, c.p. e la norma civilistica di pari grado dell’art. 1815, comma 2, c.c. comporta che la nozione del codice civile di “… (…) … interessi usurari, … (…) …” comprende sia ogni tipo di INTERESSE sia tutte le ALTRE VOCI di COSTO e la lettera “… (…) … non sono dovuti interessi” stabilisce che l’intermediario deve restituire sia ogni tipo di INTERESSE addebitato sia tutti gli ALTRI COSTI corrisposti collegati all’erogazione del credito ad esclusione dell’IMPOSTE e TASSE. Ancora, l’art. 1815, comma 2, c.c. esprime un principio giuridico valido per qualsiasi obbligazione pecuniaria e, quindi, è indifferente che la sussistenza dell’USURARIETÀ c.d. “ORIGINARIA” riguardi la clausola relativa agli INTERESSI CORRISPETTIVI o la postilla relativa agli INTERESSI MORATORI oppure ENTRAMBI i codicilli. In altre parole, dato che in caso di CONSUMAZIONE del delitto di USURA la relativa clausola è nulla e NESSUNA SOMMA è dovuta perchè il contratto diviene gratuito, la nullità della sola postilla relativa agli INTERESSI CORRISPETTIVI coinvolge il codicillo relativo agli INTERESSI MORATORI.
[1] Si legge nelle motivazioni della sentenza della Cassazione Civile, Sez. Lavoro del 24/05/1986 n. 3500 che “Gli interessi anatocistici sono dovuti sugli interessi di qualsiasi natura e quindi anche su quelli moratori(vedi per un’applicazione di tale istituto agli interessi moratori Cass. 13 febbraio 1982 n. 900; Cass. 19 ottobre 1968 n. 3371; Cass. 16 febbraio 1965 n. 252): è evidente infatti che anche questi interessi (al pari di quelli compensativi) si concreta in una somma di denaro, che, sia pure nei limiti fissati dall’art. 1283 C.C., è produttiva di interessi”. Lo stesso principio è affermato nelle motivazioni della Cassazione Civile del 13/12/2002 n. 17813: “L’art. 1283 cod. civ., che si applica anche agli interessi moratori (Cass. 24 maggio 1986 n. 3500), non consente che essi producano interessi se non in forza di convenzione posteriore alla loro scadenza, purché si tratti di interessi che siano maturati per almeno sei mesi”. Quanto alla questione che l’ANATOCISMO sugli INTERESSI MORATORI non si applica se l’interesse composto è stato pattuito con una CLAUSOLA PENALE, nella sentenza del 2002 si afferma che “quando l’art. 1224, secondo comma, cod. civ. prevede e disciplina gli effetti del patto con cui le parti predeterminano la misura degli interessi dovuti per il ritardo nell’adempimento di una obbligazione pecuniaria, altro non fa che configurare una clausola penale, con riferimento ad un tipo di obbligazione principale ed al contenuto della prestazione assunta ad oggetto della penale. Una clausola di questo contenuto non si può perciò sottrarre all’operare della regola dell’anatocismo. Questa regola si estende infatti ad ogni obbligazione di interessi dovuti per il ritardo nel pagamento di un’obbligazione pecuniaria (Sez. Un. 17 luglio 2001 n. 9653) e l’obbligazione che sorge da una clausola penale del tipo in discussione ha appunto ad oggetto quella di pagare interessi per il ritardato adempimento di un’obbligazione pecuniaria”.
[2] La norme che derogavano l’art. 1283 c.c. sono state, dapprima, l’art. 38, del Regio Decreto del 16/07/1905 n. 646. Tale deroga è stata ripresa dalla legislazione speciale che si è succeduta nel tempo, cioè dall’art. 14 del D.P.R. del 21/01/1976 n. 7 e dall’art. 16 della Legge del 06/06/1991 n. 175. La LEGISLAZIONE SPECIALE del CREDITO FONDIARIO è stata abrogata dall’art. 161, comma 1, del TUB ma continua a regolare, ai sensi del comma 6 del medesimo articolo, i soli contratti già conclusi nel vigore della stessa.
[3] Il CICR con Delibera del 09/02/2000 n. 224000 “Modalità e criteri per la produzione di interessi sugli interessi scaduti” in vigore dal 22/04/2000 al 30/09/2015 ha consentito ulteriori deroghe oltre ai casi specificati ex art. 1283 c.c.. In particolare, nelle OPERAZIONI DI FINANZIAMENTO RATEALE, in caso d’inadempimento, è consentito l’anatocismo, cioèla MORA sull’intera rata non rimborsata (QUOTA CAPITALE più QUOTA INTERESSI corrispettivi), seppur senza alcuna capitalizzazione periodica. L’art. 3 della delibera prevede infatti che “1. Nelle operazioni di finanziamento per le quali è previsto che il rimborso del prestito avvenga mediante il pagamento di rate con scadenze temporali predefinite, in caso di inadempimento del debitore l’importo complessivamente dovuto alla scadenza di ciascuna rata può, se contrattualmente stabilito, produrre interessi a decorrere dalla data di scadenza e sino al momento del pagamento. Su questi interessi non è consentita la capitalizzazione periodica. 2. Quando il mancato pagamento determina la risoluzione del contratto di finanziamento, l’importo complessivamente dovuto può, se contrattualmente stabilito, produrre interessi a decorrere dalla data di risoluzione. Su questi interessi non è consentita la capitalizzazione periodica. 3. Quando il pagamento avviene mediante regolamento in conto corrente si applicano le disposizioni dell’art. 2. 4. Nei contratti che prevedono un periodo di prefinanziamento, gli interessi maturati alla scadenza di tale periodo, se contrattualmente stabilito, sono cumulabili all’importo da rimborsare secondo il piano di ammortamento”.
[4] Si legge nella MOTIVAZIONE della sentenza della Cassazione Civile, del 20/02/2003 n. 2593 che “… (…) … in ipotesi di MUTUO per il quale sia previsto un piano di restituzione differito nel tempo, mediante il pagamento di rate costanti comprensive di parte del capitale e degli interessi, questi ultimi conservano la loro natura e non si trasformano invece in capitale da restituire al mutuante, cosicché la convenzione, contestuale alla stipulazione del mutuo, la quale stabilisca che sulle rate scadute decorrono gli interessi sulla intera somma integra un fenomeno anatocistico, vietato dall’art. 1283 c.c.” Invece nella MASSIMA è stabilito che “Le limitazioni poste dall’art. 1283 c.c. alla produzione di interessi anatocistici concernono anche il contratto di mutuo, non rilevando, in senso opposto, l’esistenza di un uso bancario in quanto questi sono usi negoziali. Gli usi contrari di cui all’art. 1283 c.c. sono usi normativi e sono quelli formatisi antecedentemente all’entrata in vigore del codice civile: il carattere imperativo della norma conduce al mancato riconoscimento di qualsiasi pattuizione o comportamento non conformi alla disciplina positiva esistente, tale da impedire quelle condizioni di fatto idonee a produrre un uso avente le caratteristiche dell’uso normativo. Non esiste alcun uso, antecedente al 1942, che consenta di derogare nei contratti di mutuo i limiti di cui all’art. 1283 c.c. Ne consegue la nullità delle clausole pattuite in deroga alla disciplina legale”.
[5] Ovviamente, non è necessaria la consecutività delle rate non pagate. Infatti, il testo dell’art. 40, comma 2, del TUB in vigore dal 01/01/1994 prevede che “2. La banca può invocare come causa di risoluzione del contratto il ritardato pagamento quando lo stesso si sia verificato almeno sette volte, anche non consecutive. A tal fine costituisce ritardato pagamento quello effettuato tra il trentesimo e il centoottantesimo giorno dalla scadenza della rata”.
VOLUME I sul portale www.youcanprint.it

In particolare, vi è tutta la costruzione matematica INEDITA di DEVIS ABRIANI sulle diverse ponderazioni dei periodi rateali (Anno Civile Corretto (365/365 e 366/366), Anno Civile Non Corretto (365/365 e 366/365), Anno Misto (365/360 e 366/360), Anno Commerciale (360/360) del Montante in Semplice e Composto, della rata costante posticipata (Francese) in Semplice (in t_0 e in t_m) e Composto (in t_0 e in t_m) e della rata variabile posticipata (Italiano) in Semplice (in t_0 e in t_m) e Composto (in t_0 e in t_m)
VOLUME II sul portale www.youcanprint.it

In particolare, si illustra: a) l’obbligo giuridico dell’uso della ponderazione dei periodi rateali dell’anno civile corretto spiegata da Devis Abriani nel VOLUME 1 PRINCIPI DI MATEMATICA FINANZIARIA BASILARI PER COMPRENDERE I FINANZIAMENTI RATEALI; b) la prova matematica/empirica che il Regime Composto (“Francese” o “Italiano”) è illecito ex art. 821 c.c.; c) la prova matematica/empirica che unicamente il Regime Semplice con impostazione iniziale in t_0 (“Francese” o “Italiano”) rispetta ad ogni istante temporale l’art. 821 c.c.; d) la prova matematica/empirica che il Regime Semplice con impostazione finale in t_m (“Francese” o “Italiano”) NON rispetta ad ogni istante temporale l’art. 821 c.c.; e) la modalità matematica/empirica corretta giuridicamente per il calcolo della Tentata Truffa e della Truffa Consumata; f) la modalità matematica/empirica corretta giuridicamente per il calcolo della Tentata Truffa Attualizzata da utilizzare per la verifica dell’Usurarietà del contratto; g) la prova matematica/empirica dell’impossibilità di determinazione dell’aliquota dell’indeterminatezza contrattuale del tasso corrispettivo se si usa il Regime Semplice con impostazione finale in t_m a causa dell’asintoto verticale; h) la prova matematica/empirica dei reati di Truffa e Autoriciclaggio di Cassa Depositi Prestiti per i finanziamenti concessi agli Enti locali.
